長野県計量検定所の計量ボーイです。
先月アップ「↓アルクマの体重が微妙に変わる話」を、続けます。
計量検定所日記シリーズ番外編「アルクマの体重が微妙に変わる話」
前回は、重力加速度の影響を掘り下げましたが、本稿では空気浮力の影響を考えます。

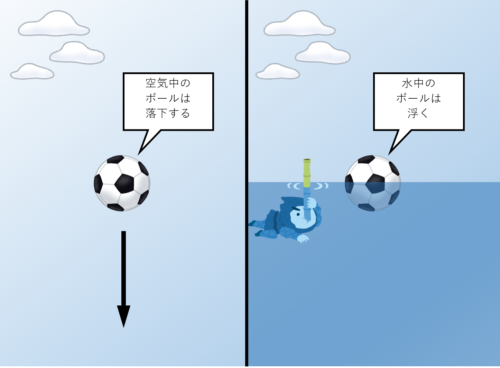
日常、同じ球体(ボール)が空気中では落下するのに、水中(面)では浮かぶことから、浮力(鉛直上向きの力、押し上げる力)の働き大小が感じ取れます。

球体の質量ｍ、重力加速度Ｇとしますと、
球体に働く重力＝ｍＧ　(式１)
これは、空気中でも水中でも同じですので、これに抗う浮力との勝負にて、
落下する空気中： 重力ｍＧ ＞ 空気中の浮力Ｆa　(式２)
浮かぶ水中(面)： 重力ｍＧ ＝ 水中(面)浮力Ｆb　(式３－１)
が導けます。

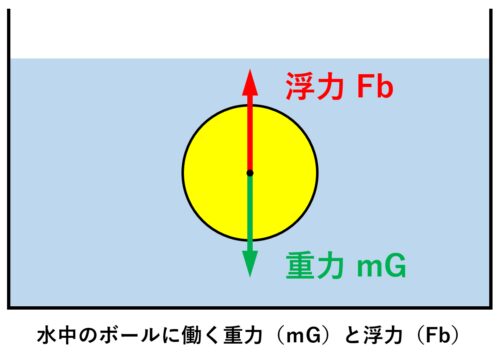
(式３－１)において、球体の質量ｍに重力加速度Ｇを掛けた重力ｍＧと、
水中(面)浮力Ｆbは逆向きで大きさ等しい力ですので、水から球体に働く浮力の大きさは、
→球体に排除された分の水(体積Ｖ)の重さを押し上げる力
と表現できます。以上、アルキメデスの原理を回りくどく説明しました。

一方の(式２)では、ｍＧがＦaを上回る大きさであるため、球体(ボール)が落下してしまいます。
更に、(式３)の釣り合い数式を、アルキメデスの原理どおりに噛み砕きます。排除された分の水の体積Ｖ(㎥)に、水の密度ρ(kg／㎥)を乗じたρＶがｍと等しい式まで辿り着きました。
ｍＧ＝ρＶＧ＝Ｆb　(式３－２)
気体と液体を総称して流体と言いますが、アルキメデスの原理は流体全般に成立しますので、
(式３－２)におけるρＶは物体によって排除される流体の密度×体積です。
→流体が空気ならば、密度 約1.2 (kg／㎥)
物体によって排除される流体(空気)の体積(㎥)＝物体の体積(㎥)

お待たせしました。
フワフワさんのアルクマ(前稿で体重20kgと仮定)、ここで登場です。

フワフワのアルクマ（身長150㎝、体重20㎏と仮定）

計量女子さん調査で↓、身長は約150cmまでは分かるのですが・・・
計量女子の計量検定所日記「アルクマのプロフィールから語る単位の話」

体積の把握を種々試みましたが、残念ながら辿り着けませんでした。
手っ取り早い方法は、浴槽を水満杯にして、アルクマが頭含め全身潜水し溢れた水の体積を量れば済むことなのですが。
※ その際の単位換算：1,000cc ＝ 1,000㎤ ＝ １ℓ ＝ 0.001㎥
長野県民手帳2021年　資料編80～81頁参照

20㎏分銅と体重20㎏（と仮定）のアルクマ

不完全燃焼ではありますが、精密な秤を使ったアルクマ20kg指示値の真の質量を、20kg分銅との比較で求めます。
分銅の真の質量　　　　　　　 ：20(kg)
その20kg分銅の体積　　　　　 ：Ｖ小(㎥)
指示値20kgアルクマの真の質量：Ｍ真(kg)
その指示値20kgアルクマの体積 ：Ｖ大(㎥)
空気の密度　　　　　　　　　 ：1.2 (kg／㎥)

20－1.2×Ｖ小 ＝ Ｍ真－1.2×Ｖ大
Ｍ真＝ 20－1.2×Ｖ小＋1.2×Ｖ大
Ｍ真＝ 20－1.2×(Ｖ小－Ｖ大)
Ｍ真＝ 20－1.2×(マイナス項)
Ｍ真＝ 20＋1.2×(プラス項)＝ 確実に20kg超の結果
※アルクマに、空気浮力が押し上げる鉛直上向き力が働き、アルクマ真の質量20kg超が
指示値20kgになってしまったことを導きました。

いつも通りクドクド記述になりましたが、今回ボーイからの計量閑話は、これにて読み切りでございます。